Fermat's Last Theorem 1637

For any integer "n" greater than 2, the equation: xⁿ+yⁿ=zⁿ has no non-zero integer solutions for x, y and z.

Pe romaneste, Marea Teorema a lui Fermat spune ca: Oricare ar fi n mai mare decat 2, ecuatia xn+yn=zn nu are solutii intregi, diferite de 0.

Although the statement can be easily understood by sixth graders, a proof has only been found recently by an English mathematician called Andrew Wiles. To even begin to understand it, one needs at least a master’s degree in mathematics. Here’s the full story...

You might have heard of his name in highschool and you were probably told about his numerous contributions to algebra and differential calculus. Pierre de Fermat (1601 – 1665) was however, a lawyer and the awkward combination between his mathematical skills and this profession made him famous during his time. He was friend with other well known contemporary mathematicians like Blaise Pascal or Rene Descartes and used to exchange letters with them. As a way of mocking these "professionals" he would send them theorems without including their proof, fact which made him known as the "prince of amateurs".

In such a way, this Last Theorem was proposed and to understand its implications let’s look at some specific values for n.

If n = 1, the statement turns into: x+y=z which has an infinite number of solutions. If we were to look at a geometrical representation of this equation, we’d have the following situation:

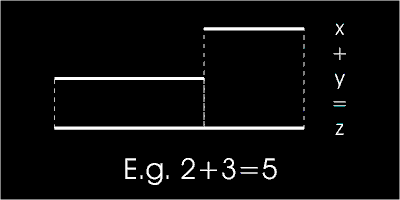
Similarly, for n = 2, the geometrical correspondents of x² and y² would be two squares and the problem would be reduced to finding a third one with an area equal to x²+y². The only limitation is that sizes of lengths x, y and z all have to be integers. This problem has been answered in Pythagoras' theorem and the solutions are the well known Pythagorean triplets:

Regular human imagination could only reach as far as the third eventual iteration if we were to continue with geometrical shapes. Moreover, the theorem states that there are no solutions for n greater than 2, so to prove it we’d have to try and imagine an infinite number of cubes and the chances of them fitting into the equation.

Over the years, systematic approaches were tried. To cover all possibilities, mathematicians tried demonstrating the formula for n=4, 5 and so on, and with the appearance of computer technology they even developed algorithms to carry out numeric calculations for higher values. Even so, there are an infinite number of (x, y, z) combinations multiplied by an infinite number of powers. That is why the final demonstration and proof found in 1994 had to use complex analytical mathematics, algebraic geometry and techniques developed in the last century.

This led many to think Fermat never had a solution to this problem. Although the current demonstration is strong proof of that, a fair number of people still believe in a "naive approach" accessible to 17^th century mathematicians. Fermat’s proof may have been based on a simple detail overlooked by all others, similarly to how 16 year old Nicolo Paganini found his pair of amicable numbers. It might have included a fairly complex algebraic demonstration left out by other mathematicians. However, the most mind-blowing possibility is that Fermat found a shortcut beyond any conventional approaches. There is a chance that a brilliant mind such as his found a corresponding abstract structure or a set of properties, that would transcend and morph from segments to squares, cubes and so on or from length to surface and volume. After all, Fermat’s original description of the problem involved a hint about geometrical shapes and the starting point of this 350 year old search was a note written by Fermat himself on the small edge of one of his books:

Cubum autem in duos cubos, aut quadratoquadratum in duos quadratoquadratos, et generaliter nullam in infinitum ultra quadratum potestatem in duos eiusdem nominis fas est dividere cuius rei demonstrationem mirabilem sane detexi. Hanc marginis exiguitas non caperet.

It is impossible to separate a cube into two cubes, or a fourth power into two fourth powers, or in general, any power higher than the second into two like powers. I have discovered a truly marvellous proof of this, which this margin is too narrow to contain.

The theorem caused many reactions and has as many implications. It has revived the ancient "liar" paradox and given birth to new problems. Some equally important ones were solved along the way and as a consequence. It scared well known mathematicians from its path, brought others to despair and all of this contributed in an ironic way to the legacy left behind by Pierre de Fermat and his eccentric view on math.

References:

• Wikipedia – Pierre de Fermat – EN, RO;
• Wikipedia - Fermat's last theorem - EN, RO;
• Wikipedia - Andrew Wiles;
• Fermat's Last Theorem - David Shay;
• Fermat's Last Theorem - Nico de Jong;
• this 45 min. documentary on Andrew Wiles’ proof (yeah, there’s a film):